Introduction
The basic building blocks of western music are the result of hundreds of years of experimentation and evolution. Through these hundreds of years of evolution, we have arrived at 12 tones in a tempered scale and 12 intervals that are used in every genre of western music. While the styles of music change, they all share these simple building blocks.
This leads us to several questions, among them, why do we use certain intervals more than others? What does the relationship between frequencies/vibrations teach us about our definition of consonance, dissonance, and harmony? Why since Medieval times did our chords evolve to chords primarily built stacking 3rd intervals? How does this affect songwriting and composition?
Let’s explore some of these questions, perhaps learning a bit more about the harmonic series and the mathematical ratios that make intervals in western music sound the way they do.
A. The Harmonic Series.
Any discussion about the evolution of western harmony would be incomplete without a discussion of the harmonic series and its implications for tonal harmony.
First off, what is a “harmonic”? It is the eerie, simple, pure sound you get when you pick a guitar string while very lightly touching that string on for example the 5th, 7th or 12th fret.
The word “harmonic” is defined as: “a component frequency of a wave”.
What does that mean: “component frequency”?
- Well the word “component” means: “a connected part of a greater whole”, or “a connected subset of a set”. Your steering wheel for example is one of the many components that make up your car.
- The definition of “frequency” is: “a number of occurrences of a repeating event per unit time”. In music, this refers to vibrations (of strings on stringed instruments, air columns in wind instruments, air molecules hitting your eardrum), which keep repeating in a regularly vibrating pattern, resulting in a produced sound that is perceived by our brain.
So a “component frequency”: is one of the many vibrations of a whole series of vibrations that combined produce a more complex sound, than each individual vibration. Hence: the harmonic series!
A great way to envision that complexity is by seeing the waves drawn out on a graph.
The wave of a harmonic looks like this: a pure, simple, single vibration.
The wave of an A 440Hz note played on a guitar string.
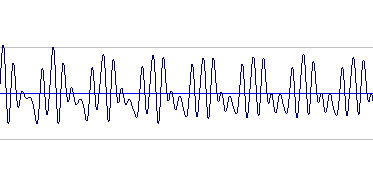
This wave is visibly more complex in shape because that string vibration consists of a whole series of sub vibrations, which is also called “the harmonic series”
Basically, the harmonic series is the series of harmonics, in order, that occurs when an individual note is played on an instrument. This is great to know about: Mother Nature mathematically organized sub vibrations (harmonics) into a well-defined structured pattern, which is what comes out when you play any single note on any instrument.
Here’s what the harmonic series looks like for a C note played on any instrument:
Just to be clear on this: when you play a C note on an instrument, you only hear a C note because the first harmonics in the series have the most energy, meaning vibrational strength, and the energy of the harmonics get weaker as you keep progressing through the series, which is why the human ear is not sensitive enough to hear all the other sounds that are contained within that 1 C note you played.
However: these lesser audible sounds, are still part of the sound you are hearing, and add to the sonic quality, fullness, and timbre of that sound.
Here’s a good analogy: when you are eating a nicely cooked meal with spices, your taste buds might not be refined or trained enough to distinguish every single spice and component that makes up the meal; but when you take out one of those spices, you will taste the difference. It will not be the same meal anymore.
The meal is an analogy for “the musical note”; the spices are “the harmonics that make up the note”. When you add a little more of one spice than another, your meal will taste saltier, or spicy, or sourer, etc.
By the same token: by amplifying (adding more energy) to certain harmonics in the harmonic series, you create a timbre (sound color) that sounds more like a clarinet, or a guitar, or a piano, etc.
B. The Mathematical Organization of The Harmonic Series.
If you look at a string that vibrates on an instrument, you see one big string motion as it is happening over the entire length of the string.
However: the human eye is not sensitive enough, to see that there are actually many other string motions, vibrations, happening within the big vibration that you can detect with your eyes.
All of these single sub vibrations within the visible vibration produce pure single sounds: the harmonics. And as all these vibrations are all happening simultaneously, that means that the note you are hearing, consists of a whole series of other sounds all happening simultaneously, and all making up the sound of that one note you are hearing.
You will see on the following graph that harmonics along the string fall in specific areas along the string.
A harmonic that is one octave higher than the open, un-fingered note lies at one half the length of the string. The harmonics fall at many different specific areas along the string, called “nodes.”
A “node” is a point of no vibration in between 2 vibrations on either side of that no vibration point.
It may be of more use to view this graphic that shows how the nodes are arranged along the length of a given string:
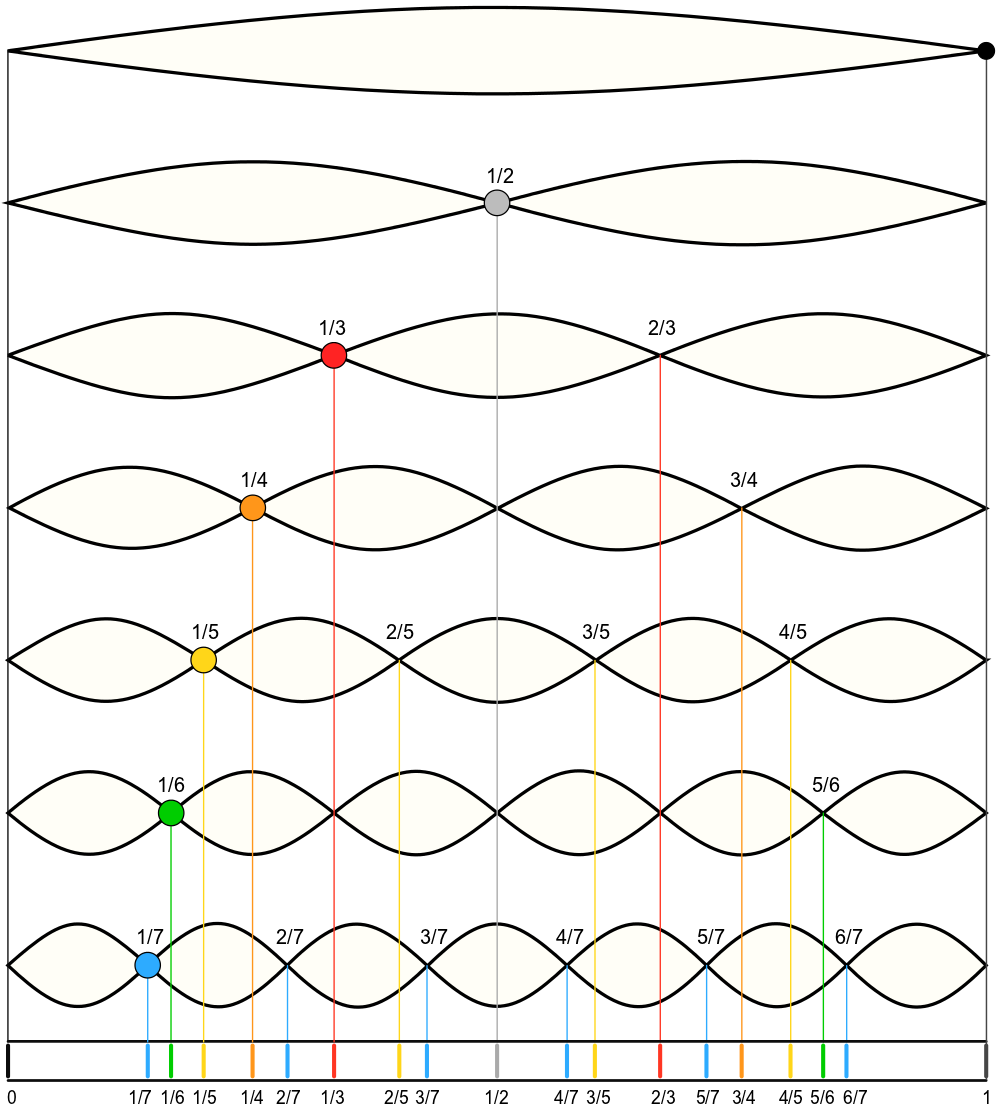
From the chart, you can see that the harmonic nodes on the string correspond to the breaking down of the length of the string into different ratios. If the first pitch corresponds to C1; the second harmonic, where the next colored dot is in this chart, is C2; the next node, at 1/3 is close to G2; the next node is C3, and so on through the harmonic series.
So all of this series is “built-in” to the sound of the fundamental note you can detect with your ears. When the entire scale length of the string is vibrating, all of the harmonic series is contained in that vibration, to varying degrees. The varying degrees to which the individual notes of the harmonic series are highlighted determine the “timbre” of the instrument. The timbre is the quality of sound that distinguishes the sound of an instrument from the sound of a different instrument.
C. The Sonic Nature of Musical Intervals Defined by The Harmonic Series.
1. The 4 Perfect Intervals: Unisons, Octaves, 4ths and 5ths.
An interval is a distance between 2 sounds. For example: the distance between C and E is a 3rd interval. It is a 3rd because there are 3 letters involved to get from the note C to the note E: C, D, E. The distance from D to A is a 5th interval because there are 5 steps, 5 letters involved: D, E, F, G, and A.
Since we only have 12 sounds in music, you can also only have 12 different distances between those sounds.
Of the 12 possible intervals, there are four intervals in western music that are called “perfect intervals”. You will find that more often than not, in most music schools when you ask your teacher: “What does that mean “perfect”? What makes those intervals perfect?” very few teachers can adequately answer that question. They will tell you that you get another perfect interval when you flip the 2 notes around, which does not really answer your question or explain anything. The reason why most teachers very often miss the target in answering those questions is that they are trained in music & composition, without being trained in the physics of sound.
We need to look at the harmonic series to really understand perfect intervals.
First off: they are called perfect because of their open, stable sound. Other analogies for the sound of perfect intervals are: sterile, transparent, hollow, colorless, etc.
The four perfect intervals are perfect unison, the perfect octave, the perfect fifth, and the perfect fourth. In the history of western music, these intervals were the first to be recognized as “consonant”. You find parallel perfect intervals in early church music, for example, such as the Organum (Gregorian Chants with simple, perfect harmonies).
a. The Perfect Unison
It looks like this on the staff, relative to middle C:
The easiest interval to explain is actually no interval at all. The unison is simply two voices playing the exact same pitch. The mathematical relationship between these two notes is necessarily 1:1, and there is no tension or anxiety produced in the listener while the unison is being played.
b. The Perfect Octave
The perfect octave, relative to middle C, looks like this on the staff:
If you were to examine the frequency of a particular pitch and double that frequency, you would produce its octave. “Doubling the frequency”, means that the string vibrates twice as often within a time frame of a second. If you have an A note tuned to the standard of 440Hz (“Herz” means “vibrations per second”), then the A note an octave lower would vibrate 220 times per second, and the one an octave below that 110 times per second.
Obviously, the mathematical relationship between the octave and the original pitch is 2:1.
The space between the original note and its octave has been divided into twelve semitones. (A “semi-tone” is the smallest distance we have in music: basically adjacent frets on a guitar, which is the same as adjacent keys on a piano. “Semi-tones” are also called “half steps”).
Again, much like the unison, the octave is an open, stable sound, and thus not known to produce anxiety in the listener.
c. The Perfect Fifth
It looks like this on the staff, relative to middle C:
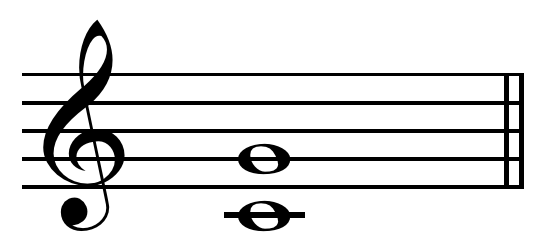
The perfect fifth is another interval that is a stable, tension-free interval when the listener hears the notes sounded together. The space between the original pitch and its fifth is 7 semitones.
The mathematical relationship between the pitches is 3:2, meaning that for every two vibrations of the original note, the upper note vibrates three times. When the two pitches are played together, the resulting sound has an open, stable, weighty sound.
d. The Perfect Fourth
The fourth, relative to middle C, looks like this on the staff:
Rounding out the perfect intervals is the perfect fourth. Again, as is typical for the perfect intervals, the fourth has an open, bland, neutral sound. This becomes useful when writing music that is not “Diatonic”. When writing modal music, for example, the composer strives to use harmony that does not use typically diatonic cadences.
One way to break away from diatonic cadences is to abandon traditional chords based on stacks of thirds. The composer can use stacks of fourths to imply his or her new modal harmony.
The space between the original note and the fourth is 5 semitones.
The mathematical relationship between the pitches is 4:3, meaning that the upper note vibrates 4 times for every 3 vibrations of the lower note.
2. Thirds And Sixths – The Beginnings of Harmony
Sometime in between the 12th and 14th centuries, musicians and composers started to realize the utility of notes other than the perfect intervals. The perfect consonance of the Organum became passé and gradually fell out of fashion. Thirds and sixths started to rise to the forefront, due to their sweet sonic characteristics.
a. The Major Third
Relative to middle C, the major third looks like this on the staff:
The distance between a note and its relative major third is 4 semitones in Western Music. The ratio between the upper note and the lower note is 5:4. Thirds are the basis of western harmony.
If you refer back to the order of the notes in the harmonic series, after the octaves and fifths, the next harmonic in the series is a major third. The third is pleasing to the ear and sounds almost sweet to the listener.
b. The Minor Third
On the staff, the minor third looks like this, relative to middle C:
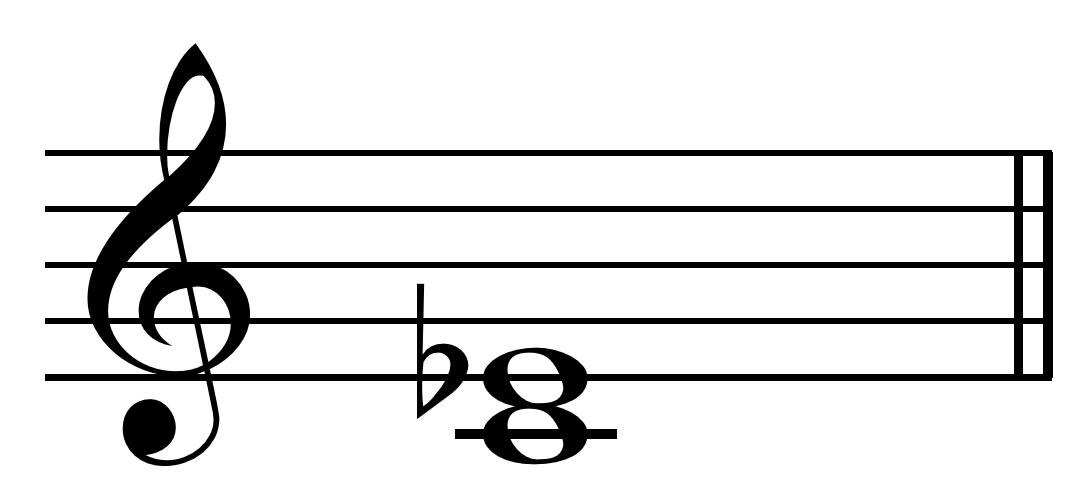
In western music, the distance between a note and its relative major third is 3 semitones. The ratio of the upper note to the lower note is almost 6:5.
Again, referring to the harmonic series, the minor third makes its appearance immediately after the major third, basically becoming the building blocks of a larger C dominant seventh chord (C E G Bb) spelled out by the harmonic series.
Where the major third was “sweet” in character, the minor third might be said to be slightly “sour”, suggesting to the listener a kind of melancholy or sad, or depressed nature.
c. The Major Sixth
Here is what the major sixth looks like on the staff, relative to middle C:
When a third is inverted, that is, when you move the lower note in the interval up an octave or the higher note in the interval down on octave, a sixth is a result. If a major third is inverted, the resulting interval is a minor sixth. When a minor third is inverted, the major sixth is produced. The distance between the notes that compose the major sixth is 9 semitones, and the mathematical relationship between the upper note and the lower note is 5:3. The major sixth’s sonic signature is related to the “sourness” of the minor third, but with a much more “open” quality.
d. The Minor Sixth
It looks like this on the staff, relative to middle C:
When the major third is inverted, a minor sixth is produced. The space between the original note and its relative minor sixth is 8 semitones, and the mathematical relationship between the upper note and the lower note is 8:5. The minor sixth’s sonic character is related to the major third, so it has a certain “open sweetness” about it.
3. Seconds and Sevenths- Tension and Dissonance
These intervals tend to add spice to the harmony, they are acidic, or sharp, and they add feelings of instability, of tension that needs to be resolved.
a. The Major Second
Here’s what the major second, relative to middle C, looks like on the staff:
The space between the notes in a major second is 2 semitones, and the mathematical relationship between the upper and lower note is 9:8. The major second has a sonic character that suggests “vinegar” but with a smooth quality.
b. The Minor Second
The minor second, relative to middle C, looks like this on the staff:
The space between the notes of the minor second is 1 semitone, and the mathematical ratio between the upper note and the lower note is 16:15. The minor second is arguably the most dissonant of intervals, very unstable. When the minor second is sounded, it suggests sharp, pungent, angriness.
c. The Minor Seventh
The minor seventh interval, relative to middle C, looks like this on the staff:
The minor seventh has the distinction of being the first dissonant note in the harmonic series relative to the fundamental. If we analyze the harmonic series in relation to the starting fundamental, we get the following intervals: Fundamental, octave, fifth, second octave, major third, second fifth, minor seventh.
The minor seventh is of course also the major second inverted. Defined in semitones, the minor seventh is 10 semitones wide, and the relationship between the upper frequency and the lower frequency is 16:9. The sonic character of the minor seventh calls to mind a kind of “sweet sourness” related to the major second, but with an openness, a smoother, less rough quality.
d. The Major Seventh
The major seventh, relative to middle C, looks like this on the staff:
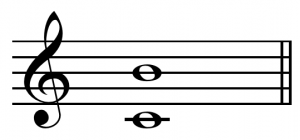
The major seventh, like its inversion, the minor second, is an interval that is reserved for instances of extreme tension in traditional western music. The space between the two notes is 11 semitones. The ratio of the upper frequency to the lower frequency is 15:8. When sounded together, the major seventh interval is not pleasant sounding. It calls to mind acidity, a caustic nature, much as the minor second, but with a slightly more open sound. In popular usage, this interval is not often used without being atop a major triad, the major triad serving to “soften” the major seventh’s “sharp edges.”
4. The Special Case: The Augmented Fourth or Diminished Fifth.
The tritone looks like this when expressed as an augmented fourth, relative to middle C in the staff:
…And it looks like this when expressed as a diminished fifth relative to middle C:
The most commonly used dissonant interval in western music is the tritone.
The tritone was regarded as an interval to avoid in the Organum of the 1200s. It is typically the most challenging interval to sing, and its usage was forbidden in medieval times. It was then called the “Diabolus in Musica”, literally translated as: “The Devil In Music”.
However: in later tonal renaissance music, the tritone, when used as part of a V7 chord, became a standard way to create tension, motion, and a feeling of instability that is about to be resolved. Depending upon how it falls in the music and on compositional context, the tritone can be written as an augmented fourth or a diminished fifth. The tritone interval is 1 fret or piano key larger than a perfect 4th, and 1 fret or key smaller than a perfect 5th.
In western music, one of the easiest ways to imply a V7 chord is to use the tritone. The listener expects the tritone to be resolved in certain ways; each note of the interval has a tendency to resolve either inwardly or outwardly to notes of the I chord in the scale.
This explains why the 5th chord, with its strong tritone interval tension embedded within the chord, always wants to resolve to the first chord of the scale. That tension-resolution characteristic created by vibrations that either sound like they are rubbing us the wrong way (when the vibrations are clashing), or that sound pleasing and thus resolved (when the 2 sound waves vibrate more in harmony with one another), is the basis that western tonal harmony is built on.
The space between the notes in the tritone is 6 semitones, and the ratio between the frequency of the upper note to the frequency of the lower note is :1. The tritone has an unstable, angry kind of feeling.
The harmonic series has played a large part in the way western music evolved. The sonic nature and feel created by 2 notes played simultaneously on an instrument, comes directly from the harmonic series of overtones in both these notes that mathematically interact in complex vibrational ways.
This series of harmonics is simply the way Nature has physically arranged the sub vibrations as mathematical integers, that all combined make up the full note sound you hear when you play a note on a musical instrument.
D. The Harmonic Series and Musical Composition.
1. The Harmonic Series and Tertial Harmony.
Why is it that historically, harmony in music developed to become a structure where chords are built stacking 3rd intervals?
If we examine the order of the harmonic series, it isn’t surprising that the intervals that sound most pleasing in western music are closely intertwined with the first eight pitches in the series. If we stack those eight notes on top of one another, built upon the fundamental C, they are: C C G C E G Bb C. When we eliminate the doubled notes, we are left with C E G Bb: these are the 4 notes that make up a C7 chord. Not surprisingly, the dominant seventh chord plays a huge role in western music and western tonal harmony.
Not only that: the notes C, E G, and Bb are all 3 steps apart (CDE, EFG, GABb) from one another.
Historically chords evolved to become tertial harmony chords because stacking notes in 3rd intervals, sounded very useful/functional, “locked in”, pleasing to our ears. The reason: these notes, 3rds apart, vibrate in accordance, or in other words “in harmony”, with the harmonics that make up the single root (C) note of the chord on which we stack 3rd intervals. The first 7 harmonics of a C note are (C, E, G, Bb), and stacking 3rds on a C note gives you the notes C, E, G, and Bb.
Conclusion: western tonal harmony is based on chords predominantly made up of stacked thirds, due to no doubt to the influence of the harmonic series on western musical conceptions of consonance and dissonance.
2. “Functional” Harmony.
Many harmony books and courses in music schools, talk about “Functional harmony”.
Entire books have been written on the subject of harmony, and a thorough discussion would be way beyond the scope of this chapter, which merely wants to explain what “functional harmony”, is and what creates that “functionality”.
The term “functional harmony” refers to the fact that all chords within a scale have and create a certain “feel” and certain tendencies within a chord progression or song. In other words: specific chords fulfill a very specific “function” within a chord progression, composition, or song. Certain chords within a chord progression feel like they don’t want to go anywhere, they feel resolved; while other chords feel like they are “on their way” to another chord they need to resolve to.
What this means when we look at the bigger picture: is that music is basically structured into a grid of “cause & effect”, “tension & resolution”, “static feel & motion”.
Since the tertial organization of harmonics in any single note, as explained above, dictated chord formation historically evolving to tertial harmony chords, one could say that chords are “locked in” into the “structural grid that mother nature” provided for the construction of musical sound.
It is that being locked in “into the grid of harmonics” provided by nature (in combination with the sonic nature of previously discussed intervals) that makes tertial harmony “functional”. The “framework” that chords are locked into, provides an organizational structure that gives chords a resolved feel or a tension feel within that framework. As such: functional harmony creates direction, storytelling, motion… all elements that make up what is called “tonal music”.
One of the best ways to fully understand this on a deeper level is by constructing chords of 4th intervals, called “quartal harmony”, and playing chord progressions with quartal harmony chords within a scale. No longer stacking 3rds, you are no longer “locked in” within the harmonic series. You could call them “outlaw chords”: they fall outside of the harmonic series organization and as a result, they could go wherever, whenever, no tendencies, no expectations. The sonic result is incredibly striking. The progressions feel like they are aimlessly floating about, wandering around, without directions, and without a sense of story. They are no longer “functional harmony”.
3. Why are Parallel 5ths and Octaves in Classical Composition Forbidden?
When you write classical music, you write to accommodate the 4 registers of the human voice, which from low to high are: bass, tenor, alto and soprano. Bass and tenor are the 2 lowest and higher registers of male voices, alto and soprano the lower and highest register female voices. Instrument groups are organized according to the human voice registers:
For example:
- Double bass (bass), cello (tenor), viola (alto), violin (soprano)
- Baritone sax, tenor sax, alto sax, soprano sax
The individual notes played by the 4 instruments, each corresponding to a register, form chords. In string quartets for example: the bass plays the bass lines, the violin plays the highest register, which is the melody, and the cello and viola fill in the rest of the chord notes in between.
Composition students spend a great deal of time in music schools, writing 4-part music to hone their composition skills and understanding of harmony.
All this leads up to explaining what “parallel 5ths” and “parallel octaves” are.
Parallel 5ths and octaves is, what you get when you have a 5th or octave interval between 2 voices in a chord, and you go to the next chord, having the same interval in the same voices in your following chord.
This costs you grades in music schools, as this is considered a composition mistake.
Starting in the renaissance, composers began to notice certain things about the effects of using tones from the harmonic series in parallel. They started to realize that the first few intervals of the harmonic series, when used in parallel, had the effect of making their music sound “colorless,” “tensionless,” or “bland.” This is something that most traditional harmony and counterpoint classes miss: there are really good reasons that parallel fifths, fourths, and octaves are avoided at all costs. The reason? Parallel perfect intervals have no sense of movement, no sense of drama, no sense of tension or release. When other parallel intervals are used, more movement, drama, and color are evident.
It’s easy to work this out for yourself. Play a simple melody. With a second voice, play a parallel melody a perfect interval (octave, 5th or 4th) away. (You could record the melody then play along with it, or harmonize the melody on your instrument on the spot).
Now to compare that sound: play the same melody again, this time in the second voice, play parallel thirds or sixths.
Now for the interesting part: play that melody again, but this time use a combination of sixths, thirds, and perfect intervals, taking care at some point to intentionally not use parallel perfect intervals in your second voice. Notice the way that sounds. Finally, play the original melody, then in the second voice, use some combination of thirds, sixths, and perfect intervals, this time intentionally using parallel perfect intervals at some point. Notice how that sounds and feels.
Hopefully, you will notice that the parallel perfect intervals leave this yawning chasm in the music, like a trapdoor that has suddenly opened beneath you, leaving you floating, with not much to relate to…until the next sixth or third rolls around. Interesting.
4.Jazz and Extended Harmony
At the beginning of the 20th Century, popular songwriters in America began to become bored by triads and traditional dominant seventh chords. They started to extend the stacked thirds of tertial harmony, making 5, 6, and 7 note chords. Here’s an example of a Cmaj13 Chord with all possible diatonic tensions in a tertial stack:
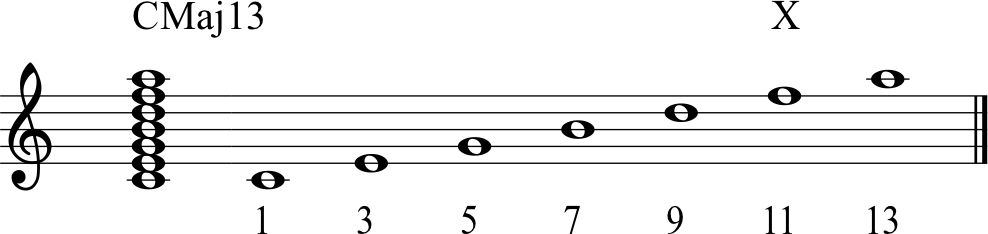
You’ll find that when you play this chord as written, there is a really unpleasant dissonance caused by the 3rd, E, “rubbing” against the 11th, F. Therefore, when most modern musicians play a Cmaj13 chord, they will omit the 11th.
Jazz harmony has evolved with its own trajectory and its own guidelines since the beginning of the 20th Century. Jazz composers have basically abandoned the doubling of the first few frequencies of the harmonic series in favor of replacing them with more “interesting” notes. They have come to refer to these interesting notes as “tensions.”
The most “pleasing” tensions that there are in Jazz harmony are one whole step away from a chord tone. By this definition of “consonance” in Jazz, we will notice a few things.
First, we notice that in chords based on a major triad, defined here as 1, 3, and 5, the tensions that sound the best are: 9, or one whole step above the root (= octave, “octo” = 8 + 1 = 9); #11, or one whole step above the third, and 13, or one whole step above the fifth. Sevenths are not included in this definition, because the seventh is a defining tone of the sound of the chord, and if we’re speaking of a tension that would lie one whole step above the major seventh, that would be a b9, or a Db relative to C. Try that.
Play the following chord: C E G B Db. Sound good at all? Still, have the “major seventh-ness” that you are used to hearing in your favorite Jazz recordings? Probably not. Also, when we are speaking of tertial chords that have a minor seventh in them, such as Dominant Sevenths, Minor Sevenths, and Minor Seven Flat Fives, one whole step above the minor seventh is the root, which is redundant.
So, using the strictest definition of “Jazz Consonance” we can use these “legal tensions” to construct scales based on the five basic types of seventh chords, Major 7, Minor 7, Dominant 7, and Diminished 7.
a. Major 7:
If we stack out thirds up in a way that forces the three tensions to be one whole step away from the three tones of the major triad, we get this:
Arranged in a scalar fashion, this becomes:
This is a G Major Scale played from its fourth degree, or a C Lydian Scale.
Interestingly, of the first 11 tones in the Harmonic Series, 10 of them are in the Lydian Scale.
b. Minor 7:
When we construct a minor seventh chord on C, that is, a minor triad topped by a minor seventh, and then stack the upper structure tensions on top, using the strictest definition of Jazz Consonance, we get this:
Arranged in a scalar way, we get:
A Bb Major Scale played from its second degree, or a C Dorian Scale.
c. Dominant 7:
Starting with a Dominant Seventh Chord based on C, or a major triad with a minor seventh stacked on top, and then adding tensions one whole step away in strict adherence to Jazz Consonance, we get this:
Arranged to form a scale, we get this:
A G Melodic Minor Scale played from its fourth degree or C Lydian Dominant Scale.
Interestingly, of the 16 notes of the Complete Harmonic Series, only the 15th is not present in the Lydian Dominant Scale. In other words, the scale that best exemplifies the Natural Harmonic Series is the Lydian Dominant Scale. Mother Nature is a Jazzer!
d. Minor 7b5:
Again, if we take a basic Minor 7 b5 Chord, or a diminished triad topped with a minor Seventh, and add tensions using the strictest definition of Jazz Consonance, we are left with this:
Arranged to form a scale, these notes become:
An Eb Melodic Minor Scale played from its sixth degree or a C Locrian Natural 2 Scale.
e. Diminished 7:
Here’s a trickier one. If we take a Diminished Seventh Chord, that is, a diminished triad topped with a diminished seventh, we get a symmetrical chord composed entirely of stacked minor thirds. If we add tensions to his chord, adhering rigidly to the concepts of Jazz Consonance, we get this:
Or in scale form:
–The eight-note Symmetrical Diminished Scale begins with a whole step.
Even in Jazz Chord and Scale construction we see the influence of the Harmonic Series, very clearly.
How clearly you might ask?
Well… it is quite striking how harmonic number 9 in the harmonic series of a C note, is a D (which indeed is the 9th tension available on a C chord), harmonic number 11 is F# (which as you guessed, is the available tension #11 on a C chord), and harmonic number 13 is an A (which again, is the last available tension 13 on a C chord).
Mother Nature once again shows she is an avid Jazzer! She embedded all our available harmonic tensions, which we all like so much because of the harmonic richness they add to chords in jazz music, at exactly the same intervallic locations within the harmonic series. Or maybe it is the other way around? We, over centuries, organically structured our music to the highest levels of harmonic invention and mathematical structure, without being fully aware that however it evolved, was being dictated by the sonic structure of Mother Nature…. Or “The Universe” as one could call it for that matter.
The more you think of it, the more you realize how mind-bogglingly structured music is.
From the way we make complex chords by stacking thirds on one another, to the way we think certain intervals sound “good” when played as tensions over chords, the Harmonic Series has played a huge role in the way all of this evolved.
5. The Harmonic Series and Arrangement Choices
Obviously, the Harmonic Series has a huge part to play in not only the Chords and Scales of Jazz, but also in the voicing and voice leading of Jazz Pianists, Guitarists, and Horn Arrangers.
When there are only four horns or only six strings, how do you outline the sound of a complex seven-note chord without losing its essential character? You have to “sacrifice” notes: but which ones? How do you choose which notes to omit?
Again, the answer lies in the Harmonic Series. In the previous chapter we looked at adding tensions to chords; this time, however, we will be looking for tones we can leave out of chords without losing the sonic nature and feel of that chord.
When a note is sounded, the overtones of the harmonic series appear in the analysis (through a device called a “spectrum analyzer”) of that note, in order of most prominent to least prominent. For example, when we play a C, the most prominent overtones are the first four in the series: the fundamental root-note the octave above, the fifth above that, and the second octave. What that means is that those are the loudest sounding harmonics in the series, the ones that have the most energy.
You basically have 3 root notes, within the first 4 harmonics. What this means, firstly, is that there is probably not a good reason to double the root in extended Jazz Harmony chords. Secondly, since the fifth plays such an important role in the harmonic series, this means that YOU ARE HEARING THE FIFTH FROM THE ROOT’S 3RD HARMONIC, whether you want to or not.
Try this! Play a seventh chord that naturally contains a perfect fifth (Major 7, Minor 7, or Dominant 7). Now play the same chord omitting the Fifth. Did you lose anything? Pretty interesting how that note does not really make that much difference in the chord, right? Why would that be? The reason for this was discussed in the section on perfect intervals (unisons, octaves, which are basically chord roots, and 4ths and 5ths): they sound transparent and colorless.
As a result: those intervals don’t add all that much character, color, and personality to a chord. Perfect intervals just merely add some “foundation”, some “ground” to the chord. In other words: the harmonic series is the reason why you can leave roots and 5ths out of extended chords without losing that chord sound.
What these two things mean for the Jazz pianist, guitarist or arranger, is that anytime you have a chord voicing that doubles the octave, you should substitute the 9th by moving that octave up a step to the 9th. Also, anytime your normal voicing contains the fifth, substituting the 13th by moving the 5th up a step, is a better way to go.
In fact, since most Jazz is played with a bass player, when you are playing chords and accompanying a soloist, it is probably better to not play roots at all. The bass is already playing the root, so any root you play is redundant.
The Harmonic Series and its strongest overtones free up the Jazz player to use more interesting notes to make more colorful music, expanding the musician’s abilities beyond the limitations of their instruments.
6. Rock, Distortion, and the Harmonic Series
Rock music has evolved in a different direction. While Jazz had made use of the Harmonic Series to make more colorful music with more upper structures and more use of stacked thirds, Rock music has simplified, largely due to the way the Harmonic series works when played through an amplifier with large amounts of distortion.
When a vacuum tube amplifier is driven hard, the sine wave of the guitar sound gets slightly compressed, rounded off, or “clipped.” Depending on the style of the amplifier, the clipping of the sine wave causes either the odd-numbered Harmonics or even-numbered Harmonics to be accentuated.
This is called distortion. “Distortion” is the result of the amplifier adding harmonics that aren’t normally heard in a non-distorted guitar. What this does is make guitarists that use distortion simplify the chords they play, so the chords they play are clear and do not sound “muddy.” The way that most Rock and Metal guitarists solve this problem is to play “Power Chords.”
Power Chords is a name for a particular style of voicing guitar players use that contains almost NO harmonic information. Usually, the voicing consists of a Root note, the Fifth above, and the Octave above the root. Like this:
When played with no distortion, this chord sounds sort of thin and ambiguous, but when distortion is applied, the added content from the Harmonic series makes this chord sound thicker and more powerful. When any other tones are added to this basic chord, the added harmonics start to clash with each other and the end result is a chord that sounds muddy, diffuse, and decidedly not powerful.
In Rock and Metal, power and clarity are the names of the game, and through the effective use of the Harmonic Series, these guitarists are able to harness the harmonics to achieve their goals.
Conclusion
Western Music, in all its forms, has evolved to sound the way it does now largely due to the influence of the physics of the Harmonic Series. In most traditional harmony classes, teachers do not recognize the role the Harmonic Series has played in our definitions of consonance and dissonance. In most cases, we are told to avoid parallel fifths and octaves as a rigid rule, with no adequate explanation as to WHY we should avoid them. All these answers lie in the analysis of the Harmonic Series.
As music students, we should keep the Harmonic Series in mind, as it ties everything in Traditional Western Harmony, Jazz, and Distorted Rock music together.
Learn the physics of the Harmonic Series, learn WHY certain pitches sound good together, learn WHY the musical genre you gravitate toward has evolved to sound the way it does and use that knowledge to make better music.
It is not “essential” that you know all of this… but isn’t it fascinating to know how Mother Nature played such a large role in our music and doesn’t it make you appreciate music on an even deeper, mysterious level? Learning about all of this does not “take away” the magic; on the contrary: it makes the musical journey progressively more magical and mysterious as you keep delving deeper and deeper into it.
Have fun further getting lost into all the mystery that is music.
Conclusion
Hit me up anytime at vreny@zotzinmusic.com if you have any questions, or if you would like to book a lesson.
These free lessons are cool, but you will never experience the progress, joy, and results that my students experience in lessons when you’re learning by yourself from blogs and videos.
That is why people take lessons: way better results and progress, much more complete information, exposed to way more creative ideas than you can get from a blog or YouTube video.
There is only so much that self-study can accomplish.
If you want to see amazing results and progress in your guitar playing, buy your first lesson here and get started ASAP.
- 1 Lesson = 75
You’ll impress your friends and loved ones in no time with your guitar playing!
Consider donating any small amount to help me keep this blog going.
Thank you for your support!
(6 votes, average: 5.00 out of 5)
